Sehr geehrte Damen und Herren! |
|
 Einige Tage vor Weihnachten 1900 hielt Max Planck seinen berühmt gewordenen Vortrag über die Quantelung der Eelektromagnetischen nergie vor ausgewählten theoretischen Physikern. Planck hatte die Idee von der Körnigkeit der Energie von Boltzmann übernommen, ja er verdankte sogar seinen Lehrstuhl diesem Meister der mathematischen Physik. Einige Tage vor Weihnachten 1900 hielt Max Planck seinen berühmt gewordenen Vortrag über die Quantelung der Eelektromagnetischen nergie vor ausgewählten theoretischen Physikern. Planck hatte die Idee von der Körnigkeit der Energie von Boltzmann übernommen, ja er verdankte sogar seinen Lehrstuhl diesem Meister der mathematischen Physik. Zu diesem Zeitpunkt war aber die Körnigkeit der Materie, gemeint sind Atome, noch nicht allgemein akzeptiert. Planck war sich somit im Klaren, dass er das Dogma „natura non saltat“ angriff und glaubte, seine Kollegen durch seine exakte Beweisführung überzeugen zu können. Während er also an die Ratio appellierte, war er sich des psychologischen Momentes im Sinne von Gustave le Bon nicht bewusst, dass nämlich die Menschen grundsätzlich nicht gewillt sind, sich von der Wahrheit einer neuen Idee überzeugen zu lassen. Das Ergebnis war eiskaltes Schweigen. Einer Notiz seines Sohnes zufolge wurde er 5 Jahre lang von seinen Kollegen nicht mehr gegrüßt, die akademische Attitüde deutlich zu machen, dass man eine Person für verrückt hält. Ich stehe hier heute vor Ihnen und habe keine Hypothese entwickelt wie damals Planck. Er hatte übrigens das Glück, dass 1905 ein junges Genie ohne akademischen Abschluss das Rätsel der Elektronenemission durch Lichteinwirkung mit der Formel E = h·ν angepackt hatte. Jetzt lockte für Planck plötzlich der Nobelpreis. Ich habe, um es zu betonen, auch keine neue Theorie entwickelt, denn die moderne Physik erstickt an neuen Theorien. Ich stehe hier und leite die Revolution unseres physikalischen Weltbildes ein, indem ich über die Logik, die Grundlage allen Denkens und Reflektierens über die Natur, die Mathematik neu fundamentiere. |
Der Inhalt des Vortrags handelt von der Bedeutung der Primzahlen als Anzahlen für die Struktur des vierdimensionalen Raumes und von logarithmischen Primzahlen als Hintergrund für den dreidimensionalen Raum, was im Verlauf des Vortrags erläutert werden soll.
Wenn sich das Rad der Geschichte dreht, wird niemand gefragt. Aber ich will wegen Plancks schlimmer Erfahrung nicht an Ihren physikalischen Sachverstand appellieren, sondern an Ihre Herzen. Sie waren einmal jung und wollten Physik, Chemie oder Ingenieurwissenschaften studieren und träumten gar von einer akademischen Laufbahn. Diejenigen von Ihnen, die es geschafft haben, wissen, dass die Jugendträume von der Realität, der Routine, den Vorlesungen und endlosen Sitzungen und auch von der Familie und dem Alltag verweht sind. Öffnen Sie Ihre Herzen und seien Sie eine Stunde wieder jung. Das Rad der Geschichte hat sich gedreht; denn ich bin als erster hinter das Geheimnis der Natur gekommen. Das Universum ist, so wie Galilei es formuliert hat, in Mathematik geschrieben. Das Planck’sche Wirkungsquantum war immer schon da. Planck hat es nur gefunden und nicht erfunden. Galileis und Keplers Ansichten über das mathematische Wesen der Natur stammen von Plato, der den Satz formuliert hat, dass hinter der Welt ein völlig verborgener, transzendenter, mathematischer Bauplan steckt. Sein Schüler Aristoteles hat den Gedanken seines Meisters verworfen, und so durchzieht das Abendland seit 2300 Jahren die Dialektik vom Bauplan und den ewigen Ideen einerseits oder die krasse Ablehnung jeder Planung andererseits. Deutschland war einst das Mekka der Physik, und dann hat eine Tollwut unserer Politiker es erreicht, dass wir das Weltbild der anglo- amerikanischen Sieger übernommen haben, die die Rätsel dieser Welt mit dem Zufall „erklären“. Die Aufklärung hatte Thomas von Aquins Schöpfung „ex nihilo“ der Lächerlichkeit preisgegeben, und jetzt sind wir mit Superstrings, 11 Dimensionen und Schöpfung der mathematisch- physikalischen Naturkonstanten aus dem Urknall wieder beim „ex nihilo“ angelangt. Öffnen Sie Ihre Herzen und seien Sie einfach wieder 15 Jahre alt, so wie ich dies auch einmal war und beim Lesen von Platos Höhlengleichnis vom Schock getroffen wurde. Aus meinen Kenntnissen in Chemie und Physik erfasste ich schlagartig, dass wir nur die Schatten der Wirklichkeit sehen, und dass endlich einmal, im Sinne einer Pflichterfüllung, einer die Aufgabe übernehmen muss, die sich mit der Frage befasst, was ist Wahrheit und Wirklichkeit. Ich wusste damals, dass es dazu notwendig war, Chemie und Physik zu studieren und zu lernen, den Mund zu halten. Eine entscheidende Beobachtung brachte mich mit 28 Jahren in ein von nun an atemberaubendes Forscherleben. Ich hatte damals die Weinsäure gewissermaßen in Silizium nachgebaut. Mit dieser Säure hat Louis Pasteur die Stereochemie begründet, die später ein Eckpfeiler der Biochemie und der Pharmakologie werden sollte. Von diesen beiden Fächern wusste ich noch nicht, dass ich sie später auch studieren würde. |
Sie sehen das Siliziumgrundgerüst der Weinsäure und zwar zwei sich gegenüber stehende Siliziumatome. Beide Atome besitzen ein freies Wasserstoffatom; folglich muss die Verbindung aus zwei verschiedenen Grundgerüsten bestehen. Da die beiden Protonen gleich sind, müsste im NMR- Spektrum ein Singulett gemessen werden. Ich vermutete aber, dass die Siliziumzwillingsatome das Protonensignal aufsplitten und der Schreiber ein Doublett zeigen würde. Ich kam auf diese merkwürdige Idee, weil ich selbst einen Zwillingsbruder habe, der gewissermaßen mich asymmetrisch, also völlig umgekehrt widerspiegelt.
An einem bestimmten Tag lief der Schreiber des Kernresonanzspekto- graphen, setzte zum Sprung an, um die erste scharfe Linie zu zeichnen. Oben angekommen zitterte der Schreibkopf, also weder ein Singulett noch ein Doublett. Sowohl der Chef der anorganischen Chemie wie der Direktor der organischen Chemie meinten amüsiert: „Da ist Dreck drin.“ Ich zitterte auch einen Moment vor Wut und kaufte dann ein Kg Germaniumpulver für 2000,- DM, nach heutigem Wert – nach dem Geldverfall – etwa 5000 Euro. Kurze Zeit später schoss mein Doktorvater in mein Labor mit den Worten: „Wie können Sie…?“ Meine Antwort war lapidar: „Ich werde mit den beiden größeren Germaniumatomen beweisen, dass die beiden Spiegelformen sich energetisch unterscheiden. Ich brauche eine Handvoll Mitarbeiter und einen hoch auflösenden NMR- Spektographen für 1 Million DM.“ |
2 Jahre später lief erneut ein Schreiber, schnellte hoch, runter und wieder hoch und wieder runter. Während alle gratulierten, war mir etwas Grundlegendes klar geworden! Elektronenpaare, die sich gegenüber stehen, nennt man Elektronenpaarzwillinge. Sie haben in der Regel den Spinwert von + ½ und – ½. Arnold Sommerfeld hatte nämlich das Plancksche Wirkungsquantum mit den physikalischen Dimensionen Joule · sec durch die dimensionslose Konstante π geteilt. Damit konnte er zeigen, dass sich eine Wirkung in einen Drehimpuls verwandelt. Die Warum- Frage war dabei auf der Strecke geblieben.
|
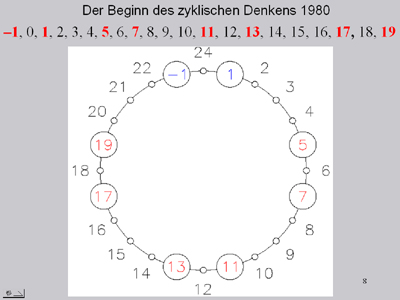
Ein Blick in einem Schwimmstadion auf die nummerierten Startblöcke mit ihren roten ausgemalten Ziffern brachte mich auf die zündende Idee, dass auch Vorstellungen nicht substanzieller Art sich umkehren, wenn sie sich gespiegelt gegenüber stehen. Das Bild zeigt die ± 1 einmal ohne Vorzeichen umgekehrt. Mir war klar, dass die Wurzel aus 1 gar keine negative 1 ist, sondern eine Spiegelung, sodass ich diese 1, herkömmlich als – 1 geschrieben, zur Folge der natürlichen Zahlen hinzufügte. Um die 0 spiegeln sich also die Wurzelausdrücke von 1.
6 Zahlen weiter lautet der erste Primzahlzwilling 5 und 7. Dieser ist schon Leibniz bei seinen zahlentheoretischen Untersuchungen aufgefallen. Leibniz war auf der richtigen Spur; denn nach der Formel 6n ± 1 entstehen die weiteren Primzahlzwillinge 11/13 und 17/19, sodass der Code mit der Zahl 24 – 1 abbricht, weil nun aus kombinatorischen Gründen Produkte von vorausgegangenen Primzahlen entstehen müssen.
|
Warum ist Leibniz nicht auf die Idee gekommen, den unendlichen 6er Takt der Primzahlen mit ± 1 beginnen zu lassen? Die Antwort ist sehr einfach: Im Zeitalter des Barocks galt die Zahl – 1 als Verstoß gegen die Logik; etwas Kleineres als 0 konnte es nicht geben. Natürlich waren die negativen Zahlen bekannt, aber nur im debitorischen Sinne.
Wenn wir die Folge der natürlichen Zahlen mit der umgekehrten 1, hier als – 1 dargestellt, beginnen lassen, kann man sofort erkennen, dass die ± 1 die Stammzahl aller Primzahlen bis in die Unendlichkeit sein muss. Natürlich ist jetzt die Frage erlaubt: Was wird aus den Zahlen 2 und 3? Die 2 ist die einzige gerade Primzahl, und die 3 ist die einzige ungerade Primzahl, die nicht von der Form 6n ± 1 ist. Nach den Gründen dafür hat bisher niemand gesucht. In jedem Mathematikbuch beginnen die Primzahlen mit den Ziffern 2, 3, 5, 7 usw.. Sie sehen, dass bei dieser Betrachtungsweise die 1 fehlt und die Primzahlen 2 und 3 gar nicht als Ausnahmen erkannt werden können. |
|
Ab der Zahl 24 wird jetzt ein weiterer Kreis eingeführt, nämlich von 24 – 48, wobei an der Stelle der – 1 vorerst gleichzeitig die 23 steht. Aus der zyklischen Anordnung lässt sich etwas Faszinierendes ableiten. Auf dem ersten Kreis befinden sich 8 Platzhalter für Primzahlen von der Form 6n ± 1. Wie man leicht nachzählen kann, gibt es weitere 8 3er Zahlen (3,6,9,12,15,18,21,24), sodass für die übrig gebliebenen 8 geraden Zahlen 2,4,8,10,14, 16,20,22 die Logik fordert, sie als 2er Zahlen zu bezeichnen. Folglich muss das Anfangsglied der 3er Zahlen, die 3 prim sein und das Anfangsglied der 2er Zahlen, die 2 ebenfalls prim.
|
Weil Leibniz wegen einer – 1 die Zahlen 1, 2, 3 nicht als Anfangsglieder von Klassenzahlen, den Nombre primeur K1, K2 und K3 erfasst hat, musste er auch die Primzahlen von – 1 bis 19 übersehen, was Euler und Gauß unbedingt hätten wissen müssen, als sie fortlaufende Zahlen untersuchten, die keine Anzahlen sind, sondern Steuerbefehle, gemeint sind, fortlaufende Exponenten in geometrischen Reihen.
Auch Kant hat die Dreifachheit der Zahlen nicht gekannt, sodass er dem Raum 3 Dimensionen zuschrieb und der Zeit eben nicht. Er formulierte es folgendermaßen: Räume sind neben einander und Zeiten, Vergangenheit, Gegenwart und Zukunft sind hintereinander. Da Mengen auch unendlich sind, musste er in den fatalen Irrtum fallen, die Unendlichkeit lediglich räumlich und zeitlich zu deuten. In Wirklichkeit ist die Unendlichkeit trinitär, bestehend aus Raum, Zeit und Zahlen, wobei auch die Zahlen dreifacher Art sind, weil sie sich von den Zahlen 1, 2 und 3 ableiten. |
72, 112, 132, 172, 192, 232, 252 usw. befinden. |
Während auf dem ersten Kreis zyklisch die Codezahlen 1, 5, 7, 11, 13, 17, 19, 23 stehen, müssen auf dem Strahl rechts vom Strahl 4n! die Quadrate des Primzahlcodes liegen. Deswegen muss die erste Zahl selbst quadratischer Natur sein und 12 lauten, mathematisch korrekt 1x12. Daher fordert die Logik, dass sich unterhalb der 12 eine weitere quadratische 1 befindet.
|
In der Tat fordert diese Logik, dass sich in dem leeren Kreis gegenüber von – 1 die Zahl + 1 befindet und zwar als Quadrat von – 1. Denn – 1 mal – 1 ergibt + 1. Nunmehr ist das Primzahlkreuz von einer 8er Kombinatorik geprägt, die unterhalb des ersten Zahlenkreises nur 2 quadratische 1en erlaubt.
|
Mit Abbildung 17 lässt sich nur noch der Atomkern erkennen, der von einem komplexen Raum umgeben ist. Er stellt die Unterschale der Elektronenhülle dar, die nur zwei Besetzungszustände zulässt. Ab dem Element 3 Lithium beginnt jetzt ein Schalenraum, der durch seine 8er Struktur geprägt ist. Die Abbildung zeigt überhaupt keine Zahlen mehr, sondern liefert eine Erklärung dafür, warum der Raum um einen Atom-kern schalenförmig ist.
Die Abbildung beschränkt sich nicht nur auf Primzahlen von der Form 6n ± 1, sondern beinhaltet alle Zahlen ohne sie zu zeichnen. So wie Raum und Zeit sind Zahlen auch nur Vorstellungen. Wir erfassen die trinitäre Verknüpfung der Unendlichkeit von Raum, Zeit und Zahlen. Gleichzeitig ist die Geometrie kreuzförmig. In der Trinität stellen aber die Zahlen wegen ihrer Primzahlverteilung einen höchst geistvollen unendlichen Code dar. Wer sich einmal mit der Primzahlverteilung beschäftigt hat, wird bei einer linearen Denkweise durch den Wirrwarr der insgesamt abnehmenden Primzahlen von Ratlosigkeit überfallen. In Wirklichkeit ist die Primzahlverteilung von einer kombinatorischen Ordnung, nur mussten die beiden Zahlen 2 und 3 von der unendlichen Menge der Primzahlen von der Form 6n ± 1 getrennt werden. Raum, Zeit und Zahlen um einen Punkt sind unendlich. Während der Raum und die Zeit eher diffuse Begriffe sind oder im Sinne von Kant nicht wegzudenkende Vorstellungen, bietet die Primzahlverteilung als ewige Ordnung die Möglichkeit, das was sich in Raum und Zeit befindet, nämlich das Stoffliche zu codieren. Da sich die mathematischen Konstanten e, i und π aus Primzahlen ableiten lassen, war ich zu der Möglichkeit vorgestoßen, die Welt sowohl im Kleinen, wie im Großen auf eine Primzahlcodierung zurückzuführen. Erst einmal räumte ich mit der fatalen Vorstellung von Einsteins Verknüpfung der 3- Dimensionen des Raumes und einer sog. 1- dimensionalen Zeit auf. Der Eulersche Einheitskreis oder die komplexe Zahlenebene besteht aus einer kreuzförmigen x, y- Geometrie. Da sie keine z- Achse haben kann, bildet sie bei ihrer Quadratur 2 sich schneidende Flächen, die dadurch gekennzeichnet sind, dass sie in der Mitte komplex sind. Die Quadratur der ± 1 Linie liefert die 12, – 12- Fläche, während die Quadratur die ± i Linie die Quadratzahlen + 1 und – 1 liefert. Die x2, y2; - Geometrie ist der 4- dimensionale Raum um einen Punkt. Der unendliche Raum muss substanzielle Punkte besitzen, sonst wäre er ein Nichts. Diese Punkte sind an jeder Stelle Mittelpunkt des Universums. Der Gedanke stammt von Giordano Bruno und Leibniz und wurde von Fichte übernommen. Die Punkte selbst müssen von endlicher Größe sein, sonst wäre die Logik verletzt. Um es noch einmal zu wiederholen. Bisher war bekannt, dass alle chemischen Elemente größer der Ordnungszahl 2 eine Unterschale besitzen, die nur 2 Elektronen aufnehmen kann. Die äußerste Schale der Edelgase ist von einer 8er Struktur geprägt. Somit ist die Schalen-theorie, die auf Bohr, Sommerfeld, Pauli und Schrödinger basiert zum ersten Mal auf eine räumliche Vorstellung gebaut, die sich aus der Geometrie der Primzahlen ableitet. Gleichzeitig wird das Periodensystem der chemischen Elemente mit seinen Haupt- und Nebengruppen erklärbar, wie wir später sehen werden. Ein Satz zu Albert Einstein: Hätte Poincaré, der letzte große Mathematiker im Range von Euler und Gauß, diesen Zahlenraum gekannt, wäre die Einsteinsche Raum- Zeit- Verknüpfung, die er aufs Schärfste verurteilt hat, durch eben diesen Mathematiker unterbunden worden. |
Wir wollen uns noch einmal mit den Quadraten der Primzahlen auf dem 1er Strahl beschäftigen. Werfen wir einen Blick auf den Zahlenstrahl oberhalb der 12; finden wir für die 2er Abstände eine Abstandscodierung. Für die 2er Abstände ergibt sich die Differenzenfolge 0, 0, 1, 2, 3, 4, 5... . (Der Abstand von –12 zu 12 beträgt 0, ebenso der Abstand von 5² zu 7², während der Abstand von 112 zu 132 1 beträgt, usw.) |
Für die 4er Abstände erhalten wir die Differenzenfolge 0, 2, 4, 6, 8… . (Der Abstand von 12 zu 52 beträgt 0, der Abstand von 72 zu 112 beträgt 2, usw.) Das ist nicht nur das Doppelte der Zahlen 0, 0, 1, 2, 3, 4, 5 …, sondern, wie sich leicht beweisen lässt, das 20fache. Aus dem Code der 2er Abstände der Quadrate der ersten Primzahlzwillinge und der zweiten Codierung der 4er Abstände zwischen den Primzahlzwillingen (z. B. 72 zu 112) lässt sich der Beweis antreten, dass der
4-dimensionale Raum um einen Punkt im Dezimalsystem angelegt ist. Dazu werfen wir kurz einen Blick auf das Periodensystem, und zwar nur auf die Hauptgruppenelemente. Der Wasserstoff lässt sich weder in die 1. noch in die 7. Gruppe einordnen, dann kommen bis zum Calcium mit der Ordnungszahl 20, 19 Hauptgruppenelemente und anschließend vom Element 31 bis 83, dem letzten stabilen Element, noch einmal 19 Hauptgruppenelemente. Warum das so sein muss, ließ sich beweisen. Dazu war es notwendig, aus den „disquisitiones arithmeticae“ von Gauß etwas heraus zu entdecken, was dieser in seiner Jugend übersehen, und was er später mit ins Grab genommen hat. Die „Disquisitiones“ sind nämlich von der französischen Akademie der Wissenschaften als obskur zurückgewiesen worden. Die größte geniale Leistung der Mathematikgeschichte ist von einem Haufen von Ignoranten falsch eingeschätzt worden. Aber noch schlimmer ist, dass wir in den heutigen Zeiten unseren Studenten verheimlichen – J’accuse –, dass z.B. die stabilen Elemente in genau 10 Sorten von Isotopen aufgesplittet sind. Sie sehen hier einen Ausschnitt aus der Nuklidkarte, wobei die Neutronenzahl 123 fehlt. In der Nuklidkarte fehlen insgesamt 8 Neutronenzahlen, was in Lehrbüchern schweigend übergangen wird. |
Eine weitere Unterlassungssünde war es, nicht deutlich herauszustellen, dass mit den Elementen Technetium 43 und Promethium 61 zwei primzahlige Neben-gruppenelemente im Periodensystem fehlen. (Es sei daran erinnert, dass sich die Haupt- und Nebengruppenelemente der Elektronenschalentheorie ebenfalls auf den Zahlen 2 und 8 aufbauen.) Durch die Herstellung von künstlichen Isotopen, die entweder Elektronen oder Positronen abgeben, ist mit einem Blick ersichtlich, dass die beiden genannten Elemente im unendlichen Universum nicht vorkommen können.
|
Die Unterschlagung bot mir die Möglichkeit bestimmte Chemiker und Physiker nicht mehr als unfehlbar einzuschätzen, sondern als Menschen. Somit hatte ich eine Chance, das Periodensystem der Elemente als mathematischen Bauplan aufzufassen. Wenn im Periodensystem 2 Elemente fehlen müssen, dann muss man sie auch von den 83 stabilen Elementen subtrahieren. 83 – 2 liefert den Wert 81, was als Potenz der Zahl 34 entspricht. Jetzt begann ich das System zu durchschauen: Alle stabilen Elemente bestehen aus nur 3 Teilchen, Protonen, Neutronen und Elektronen, wobei den Elektronen 4 Quantenzahlen zugeordnet werden, ohne zu wissen, warum.
|
|
Die Zahl 81 birgt ein schier unglaubliches Geheimnis. Ihr Kehrwert beträgt nämlich 0,012345679…, eben genau jene Zahl, die wir auf dem Primzahlkreuz als Differenzen entdeckt haben.
|
Bei diesem periodischen Dezimalbruch fehlt die Ziffer 8. Dieses Dilemma konnte ich mithilfe einer Idee des französischen Mathematikers Cauchy beseitigen. Der periodische Dezimalbruch lässt sich nämlich in einen unendlichen Dezimalbruch verwandeln 0,0123456789(10)(11)(12)…, bei dem die Zahlen größer als 9 mit Klammerausdrücken geschrieben werden müssen. Im Kehrwert der Anzahl der stabilen Elemente 81 = 34 steckt dezimal die gleiche Ordnung, die wir auf dem Primzahlkreuz als Abstände für die Quadrate der Primzahlzwillinge nachgewiesen hatten.
(Proton, Neutron, Elektron, das ist die Zahl 3, aber das Primzahlkreuz ist vierdimensional: hoch 4.) Die Computeranimation zeigt sehr schön die beiden rechtwinkligen Zahlenkreise rotierend um den 2-dimensionalen Eulerschen Einheitskreis. Warum die Natur die beiden Metalle mit den Ordnungszahlen 43 und 61 auslassen muss, hat mit einer Verschlüsselungskombinatorik zu tun, die ich 1986 brechen konnte und ähnlich wie Gauß für mich behalten hätte, wenn nicht …, aber davon später. |
Wenden wir uns nun dem Hauptmerkmal der Quantenmechanik, der Edelgasschale zu. Sie besteht immer aus einem
s- Elektronenzwilling und drei
p- Elektronenzwillingen.
|
Wenn die Atomphysiker der ersten Periode des 20. Jahrhunderts schon nichts über die Struktur des Raumes wussten, so hätten sie wenigstens ein Merkmal des 4- dimensionalen Raumes untersuchen sollen. Alles, was wir über den Raum bisher wissen, ist die Kenntnis über die Perspektive bzw. das Newtonsche reziproke Quadratgesetz.
|
Indem Physiker wie Sommerfeld, Rydberg und Pauli die quadratische Natur der Hauptquantenzahlen bemerkten, hätten sie in den Anzahlen der Elektronen leicht die Umkehrung des reziproken Quadratgesetzes erkennen können. Die 4 Hauptquantenzahlen lauten bekanntlich
2 · 12, 2 · 22, 2 · 32 und 2 · 42. |
Wir wollen die Elektronenschalen noch einmal 2- dimensional betrachten und die Zahlen des 1. Kreises als Mengen untersuchen und zwar etwa als Anzahl von Reiskörnern. Eine kurze Überlegung zeigt, dass sich auf dem ersten Kreis die Zahlen von 0 bis 24 befinden, die auf-addiert den Wert 300 · 12 liefern, was sich dezimal als 3 · 12 · 102 darstellen lässt.
|
Wenden wir uns dem 2. Kreis zu mit den Anzahlen 24 bis 48, erhalten wir das 3- fache von 300 und auf dem 3. Kreis das 5- fache von 300, so dass sich auf dem 10. Kreis das 19- fache von 300 befindet.
|
Wenn wir die ersten 10 ungeraden Zahlen aufaddieren, beträgt die Summe 100. Werden nun die ersten 10 Zahlenkreise zu einer Menge gebündelt, würden die nächsten 10 Zahlenkreise die
3- fache Summe davon ergeben und die darauf folgenden weiteren 10 Kreise das 5- fache. |
Damit erhält der 4- dimensionale Raum eine Zahlenmengenausdehnungs-
konstante von der Größe 3 · 12 · 102 · 1002 · 10002… , was Sie gelegentlich einmal nachrechnen sollten. Somit ist bewiesen, dass der 4- dimensionale Primzahlraum dezimal angelegt ist, und die Zahl 81 = 34 in diesem Raum reziprok verankert ist, was sich eigentlich physikalisch aus dem Gesetz ableiten lässt, dass Verdünnungen reziprok ablaufen. Da zwischen einem Bruch, etwa der reziproken Primzahl 1/3 und der Anzahl 3 der quadratische Faktor 9 (32) steckt, ist sofort bewiesen, dass das Gesetz der Perspektive im Dezimalsystem verankert ist, und weil das so ist, haben wir 10 Finger. Kronecker’s Bemerkung, weil wir 10 Finger haben, rechnen wir im Dezimalsystem, ist gar kein Aperçu, sondern Kennzeichen von Hybris. Den Physikern stand eben in den Zeiten von Sommerfeld und Pauli nur die Mathematik zur Verfügung, die vorhanden war. Hier wird zum ersten Mal erkennbar, dass der 4-dimensionale Raum eine Zahlenausbreitungskonstante besitzt, die wir als 3-dimensionale Wesen als Lichtgeschwindigkeit empfinden und die als Naturkonstante unveränderlich ist, was die Relativitätstheorie ja unbedingt betont.
|
Wir wollen, um das Primzahlkreuz noch schärfer zu beweisen, die Naturkonstante e daraus ableiten, indem wir ein kombinatorisches Mittel verwenden. An der Stelle 1 · 12 gibt es nur 1 Möglichkeit, an der Stelle 2 · 12 gibt es 2 Möglichkeiten: 1 und 2 oder 2 und 1. Bei der Ziffer 3 existieren schon 6 Möglichkeiten in der Reihenfolge. Wir wollen aber die Ordnung 1, 2, 3 haben, also eine von sechs. Mit der Ziffer 4 tauchen 24 Kombinatoriken auf. Wer mathematisch geschult ist, erkennt sofort, dass die fortlaufenden reziproken kombinatorischen Summenglieder als Ordnung e – 1 liefern.
|
Da die Natur nicht linear angelegt ist, sondern zyklisch, müssen wir die Ord-nung auf der komplexen Zahlenebene mit berücksichtigen. Dort existieren unendlich viele Wurzelausdrücke der Zahl 1, aber nur eine Kombinatorik, sodass e – 1 um + 1 erweitert werden muss, und die Ordnung der Zahlen auf dem Primzahlkreuz selber die Zahl e darstellt, was sich aus dem Verhältnis n zu n Fakultät leicht beweisen lässt. Genauer gilt, dass es sich um die Ordnung von Primzahlen handelt, so wie ein Wirbeltier aus Knochen und fleischlicher Masse besteht. Hier ist zum erstem Mal zu erkennen, warum die Anzahl der Primzahlen unterhalb einer gegebenen Zahl nach der Gleichung x/lnx abnimmt; denn der natürliche Logarithmus hat die Basiszahl e. Doch davon später… . Newtons Ableitung der Exponentialfunktion enthielt noch den Ausdruck 1/0!, was sich durch unsere kombinatorische Betrachtung n/n! von selbst erledigt, da nämlich 1/1! = 1 ist und 2/2! ebenfalls den Wert 1 liefert.
|
Zur Beweisführung der kombinatorischen Idee, dass die Zahl e die unendlich vielen Primzahlen ordnet, wenden wir uns jetzt der Umkehrfunktion zu n!/n. Wir erhalten (n – 1!). Wenn wir zu diesem Ausdruck die Ziffer 1 addieren, erhalten wir den Satz von Wilson, den Euler als erster bewiesen hat. Er ist der einzige Satz, der von einer bestimmten Zahl aussagt, dass sie prim sein muss. Der Satz ist, wie das Zahnrädchens in einer Schweizer Uhr, Voraussetzung für das Funktionieren eines ganzen Systems.
|
Wir erläutern die Geschichte an einem Beispiel für p = 7; 6! = 720. Erweitern wir diesen Wert um die Ziffer 1, tritt die Summe 721 auf. Wir faktorisieren in die beiden Primzahlen 7 · 103 und beobachten, dass diese beiden Primzahlen auf dem Strahl liegen, der mit der 7 beginnt. Da die Zahl 720 oberhalb der 24 = 4! liegen muss, befindet sich die Ziffer 721 oberhalb des Wertes 1 · 12. Es lässt sich leicht beweisen, dass alle ausgerechneten Werte des Satzes von Wilson immer auf dem 1er Strahl liegen, und bei der Primfaktorzerlegung diese auf einem der 8 Strahlen liegen müssen. Wir wählen ein einfaches Beispiel mit den Primzahlen 53 und 101 und erhalten das Binom (2 · 24 + 5) · (4 · 24 + 5). Beim Ausrechnen des Binoms erscheinen lauter Produkte von der Form n · 4!, die wir streichen können außer der letzten 52. Die Zahl 52 liegt aber auf dem Strahl oberhalb der 12, wonach bewiesen ist, dass für den Satz von Wilson ein geometrisches Modell existiert.
|
|
Sie haben hier zum ersten Mal in der Mathematikgeschichte gezeigt bekommen, warum die Exponentialfunktion einer Primzahlgeometrie gehorcht und umgekehrt mit dem Satz von Wilson erfahren, warum es ihn gibt. Da sich der Satz von Wilson in den kleinen Fermatschen Satz verwandeln lässt, wollen wir kurz ein Beispiel, wieder mit
p = 7, untersuchen. 27–1 –1 ≡ 0 mod 7 (64 – 1 = 63), 63 : 7 = 9 Rest 0 Was den Satz von Wilson mit dem kleinen Fermatschen Satz verknüpft, ließ sich bisher nur beweisen, die Warum-Frage war ungeklärt. |
|
|
|
Ich habe über die Exponenten 0, 1, 2, 3, 4…, also über dem Wert 1, wo die Kugel nur eine Entscheidung hat, noch den Fall eingeführt, wo sie gar keine Entscheidung hat. Da 20 = 1 liefert, fragen wir jetzt nach dem Logarithmus der Zahl 0, führen den Begriff 200 = 0 ein und ver-gleichen die fortlaufenden Exponenten mit jenen Ziffern, die wir als Positionsdifferenzen 0, 0, 1, 2, 3, 4, … der Primzahlquadrate gefunden haben, aber diesmal als Logarithmen.
Nun färben wir die durch 2 teilbaren Binomialkoeffizienten rot und erkennen ein Muster, das man fraktal nennt. |
|
Sie sehen hier die Teilbarkeit durch den Primfaktor 3, den Primfaktor 5, den Primfaktor 7 und erkennen, dass das umgedrehte Dreieck mit höheren Primzahlen zu immer kleineren sechseckigen Waben führt, bis hin in das unendlich Kleine.
Beim Primzahlkreuz vergrößern sich die Anzahlen bis in das unendlich Große über die Geometrie eines rechtwinkligen Kreuzes. Wenn wir das ins Unendliche verlaufende Große umkehren, gemeint ist Potenzinvertierung, müsste eine endliche Geometrie entstehen, was mit dem gleichseitigen Dreieck auch der Fall ist. Indem wir nun die Seitenhalbierenden des Dreiecks miteinander verbinden, entsteht in der Mitte ein umgedrehtes Dreieck, aber insgesamt sind es, wie bei den 4 Quadranten eines Kreuzes auch wieder 4 gleiche Flächen, nur diesmal 4 Dreiecke. |
Wir tauchen nun in eine Welt ein, bei der die fortlaufenden Zahlen nicht mehr Anzahlen sind, sondern fortlaufende Logarithmen und vermuten, dass sich in dieser Welt der Ja/ Nein- Entscheidungen für die Primzahlen auch eine Art Faktor-isierung beweisen lässt, die bisher völlig übersehen worden ist. Ein gasgefüllter Raum kennt nur Stoßprozesse und somit Ja/ Nein- Entscheidungen. Wie es möglich ist, dass hier in diesem Saal mit etwa 1025 Gasmolekülen meine Worte in aller Akzentuierung an Ihr Ohr gelangen, ist in dem Gewuse der Gasatmosphäre physikalisch bisher überhaupt nicht erklärbar. Der Mathematiker Kummer hat Mitte des 19. Jhdt festgestellt, dass das Pascalsche Dreieck mit dezimalen Binomialkoeffizienten als Potenzen der Zahl 11 geschrieben werden kann. Statt nun aus dieser Tatsache zu schließen, dass das Pascalsche Dreieck im p – 1, dem 10er, unserem g-adischen Dezimalsystem angelegt ist, bewies er hurtig, dass das Pascalsche Dreieck in jedem Stellenwertsystem gültig ist. Gauß hat geschwiegen; der wusste, dass es gar keinen Sinn macht, gemäß der Vorstellung der Pythagoräer den Zahlen eine Realexistenz zuzuordnen, wenn die Welt nicht in einem bestimmten Stellenwertsystem angelegt ist. Die Welt ist aber, ohne dass wir das bisher bemerkt haben, in einem Stellenwertsystem angelegt und lässt sich deswegen in jedem Stellenwertsystem berechnen, was Kummer und seine berühmten Nachfolger nicht begriffen haben. Rationale Dezimalbrüche, irrationale Dezimalbrüche und transzendente Dezimalbrüche sind ohne Stellenwertsystem nicht vorstellbar, was am deutlichsten bei der Kreiszahl π erkennbar ist.
Sie sehen, dass das Pascalsche Dreieck 8- zeilig ist. Es ließ sich 1997 als Zeile für Zeile dezimal angelegt beweisen, und zwar über die Theorie der Fibonacci- Zahlen, die dahin-gehend primzahlcodiert sind, dass die Fibonaccizahl 89 beispielsweise als Ordinale die Primzahl 11 aufweisen muss. Zwischen 81 und 100 beträgt der Restwert 19. 81 + 8 liefert 89 mit dem Restwert 11. Addiert man die Werte im Pascalschen Dreieck 0, 1, 2, 4, 8, als reziproke Ausdrücke 1/2 + 1/4 + 1/8 + 1/16 … und achtet auf die dezimale Verschiebung, ergibt sich der Dezimalbruch 0,52631…. Rückwärts gelesen beginnt der 18stellige periodische Dezimalbruch mit 1, 2, 4, 8, (16)…, was dem Kehrwert von 19 entspricht. 19 ist der Restwert von 81, sodass im Pascalschen Dreieck das Verhältnis 8 : 11 leicht begründet werden kann. |
Vorher muss man jedoch erfassen, warum der Satz von Staudt existiert, wonach sich Bernoullizahlen aus Summen von reziproken Primzahlen berechnen lassen. Die Bernoullizahlen, die benötigt werden, um Potenzsummen auszurechnen, werden in der Regel mit Hilfe der Binomialkoeffizienten ausgerechnet. Warum, wusste man bisher nicht.
|
Indem ich die Indizes der Nenner der Bernoullizahlen um 1 erweiterte, ergab sich bei der Primzahlfaktorisierung der Nenner folgendes Schaubild. Personen, die visuelle Eindrücke ikonisch verarbeiten können, sehen mit einem Blick, dass sich alle Nenner durch die Zahl 6 teilen lassen, und dass sich nach der Gleichung (p – 1)/2 alle 2 Zeilen der Primfaktor 5 wiederholt, alle 3 Zeilen der Primfaktor 7, alle 5 Zeilen der Primfaktor 11, alle 6 Zeilen der Primfaktor 13, alle 8 Zeilen der Primfaktor 17, alle 9 Zeilen der Primfaktor 19 usw. Das, was in der Welt der Anzahlen den Schulkindern so anschaulich beigebracht werden kann, dass sich in den fortlaufenden Zahlen alle 5 Zahlen die 5, alle 7 Zahlen die 7 und alle 11 Zahlen die 11 usw. durch Faktorisierung wieder finden lassen müssen, muss auch, weil jede 2. Bernoullizahl gleich 0 ist, für die Welt der Logarithmen gelten.
Nur muss man natürlich berücksichtigen, dass Logarithmen nicht multipliziert werden, sondern ihre primzahligen Teiler als reziproke Primzahlen aufaddiert werden müssen, was von Staudt nicht bemerkt worden ist.
|
Werfen wir noch einmal einen Blick auf die beiden Matrizen, die später noch um 2 weitere Kongruenzmatrizen ergänzt werden und lesen in der ersten Matrix die 2. Zeile mit fortlaufenden Quadraten. Um z.B. die Summe der ersten 10 Millionen Quadrate auszurechnen, brauchen wir lediglich die Bernoullizahlen 1/2 und 1/6. Wenn wir jetzt zur zweiten Matrix wechseln und von oben nach unten die fortlaufenden reziproken Potenzen
2–1, 2–2, 2–3, usw. aufaddieren, erhalten wir über eine Formel, die auch die Bernoullizahlen enthält, den Wert für die von Euler so genannte Zeta- Funktion; er lautet π2/6. Niemand konnte bisher sagen, warum hier der Ausdruck π2 erscheint, weil Euler den Ausdruck π2n gleich mit in die Formel gezaubert hat. Es war ein schönes Stück Arbeit, dahinter zu kommen, warum Euler bei Verwandlung der Zeta-Funktion in ein unendliches Produkt eine Formel finden musste, die außer den Einsen nur Quadrate von primzahligen Basen enthält. Das ist Glanz und Elend der Mathematik, dass wir fast alles berechnen können, aber die Frage nach dem Warum so kunstvoll haben verschwinden lassen. Die hier dargestellten Matrizen mit insgesamt 4 geometrischen Reihen erlauben es, die Mathematik gänzlich neu auf der Ordnung der Primzahlen in Anzahlen und Exponenten zu fundamentieren. Ein Beispiel: Euler konnte die Zetafunktion in ein unendliches Produkt umwandeln, indem in den Faktoren der fortlaufenden Brüche ausschließlich fortlaufende Primzahlen standen. Bernd Riemann setzte in diese Produktdarstellung komplexe Zahlen ein und logarithmierte den Ausdruck. Jetzt konnte er natürlich integrieren und schuf so 6 Behauptungen. Eine davon war der Hinweis, dass die Primzahlen nach der Formel x/lnx abnehmen müssen. 1896 bewies Jacques Hadamard die Richtigkeit des Satzes, aber niemand untersuchte die Frage, was denn die Zahlen e und π und sogar i an die Ordnung der Primzahlen knüpft. |
Gauß hatte die Vermutung über das Verhältnis x/lnx schon mit 15 Jahren im Kopf und Zeit seines Lebens ver-schwiegen. Da er aus dem kleinen Fermatschen Satz die Verknüpfung von primzahligen Exponenten und reziproken Primzahlen erfasst haben muss, hatte er natürlich die Periodenlängen von reziproken Primzahlen im Kopf ge-speichert. Sie sehen hier die
p – 1-stellige Darstellung des Kehrwertes der Primzahl 97 und erfassen die 1 als 30, die 3 als 31, die 9 als 32, die 27 als 33 und die 83 als 81 = 34 plus dem dezimalen Überschlag 2 von 243 = 35 usw. Genau das hat Gauß übersehen. |
Damit ergibt sich für den Restwert von 81 zu 100 die Differenz 19 und folgende Potenzsumme als Dezimalbruchdarstellung. Es handelt sich um den Kehrwert von 81, und zwar in dezimaler Schreibweise
00123456789(10)(11)(12)… Dies ist die neue Fundamentierung der Theorie der Reihen und war bisher unbekannt. So wie die Zahl 81 reziprok im Primzahlkreuz verborgen ist, so ist im Pascalschen Dreieck der Restwert 19 gespeichert, wobei für die 0 links vom Komma der Logarithmus der Zahl 0 als 1900 in der Mathematik neu eingeführt werden muss. Wer einmal in den USA Roulette gespielt hat, weiß, dass dort neben dem Kästchen mit der Ziffer 0 noch ein weiteres Kästchen mit der Ziffer 00 besteht, der Schrecken der amerikanischen Glückspieler. |
|
|
Bei diesen Überlegungen kam ich dazu, zu erfassen, wie es passieren konnte, dass der größte Mathematiker der Weltgeschichte Carl Friedrich Gauß das Geheimnis der Kongruenzen mod 19 übersehen hat. Gerade weil er am Beispiel der primitiven Wurzel 2 mod 19 die Kongruenzen zwischen 1 und 18 mit ihren jeweiligen Exponenten untersucht hat, die er Indices nannte und explizit wie Logarithmen behandelte, hätte ihm auffallen müssen, dass die 6 primitiven Wurzeln von 19: 2, 3, 10, 13, 14, 15 sechs einzigartige Indices besitzen. Es handelt sich in wechselnder Reihenfolge um die Indices 1, 5, 7, 11, 13, 17 mod 19. Aus der Eulerschen Theorie der φ - Funktion wusste Gauß, dass φ von 19 gleich 18 beträgt und die 18 folgende Nichtteiler besitzt: 1, 5, 7, 11, 13, 17. Jetzt rächte sich, dass Leibniz den fortlaufenden 6n ± 1- Code: – 1, 1, 5, 7, 11, 13, 17, 19 nicht erfasst hatte. Die logarithmischen Indices mod 19: 1, 5, 7, 11, 13, 17 blieben in ihrer Bedeutung unerkannt. Um es zu wiederholen: nicht nur in den fortlaufenden Zahlen, die 3facher Art sind, steckt ein Code, der bei 19 abbricht, auch in den fortlaufenden logarithmischen Indices befindet sich die gleiche Primzahlcodierung.
Auf diese Weise konnte es passieren, dass die Fragestellung unterblieb, wie viel Sorten von Teilbarkeiten stecken in den Zahlen, die Steuerbefehle darstellen, den Exponenten. Bei den Anzahlen sind es 3, ihr Raum ist 4-dimensional, bei den Logarithmen sind es dagegen 4, wie wir noch sehen werden. |
3- dimensional, die wir jetzt untersuchen wollen. Wir werden nun erneut eine Vertauschung von Basis und Exponent vornehmen und erhalten als 4. Matrize quadratische Kongruenzen modulo immer höherer Primzahlen. Auch hier zeigt die Visualisierung ein Muster, sodass die Kongruenzen zwischen 13 und 31 sich paarweise kongruent darstellen lassen. Sie können jetzt die Frage stellen, warum hier nur quadratische Glieder untersucht werden, aber so wie der kleine Fermatsche Satz lehrt, dass es nur auf die Basis 2 ankommt und größere Basen als 2 höchstens einen größeren Rechenaufwand bedeuten, gilt hier, dass es nur auf den Exponenten 2 ankommt und höhere Exponenten keine weitere Erkenntnisvertiefung vermitteln. Weil Euler, Gauß, Eisenstein bis Artin vom Bau der Atome nichts wussten, konnten sie in ihrer Zeit den folgenden Sachverhalt überhaupt nicht erfassen. |
|
Warum war mir das so wichtig? Euler, Legendre und Gauß hatten die Zweifachheit der Primzahlen von der Form 4n + 1 und 4n + 3 erkannt. Insgesamt handelt es sich um jeweils 4 Zahlen-folgen. Diese 3 großen Mathematiker müssen aber ein Tuch vor den Augen gehabt haben; denn die Zahlen4n + 0, 4n + 1, 4n + 2, 4n +3 kann man auch anders darstellen. So ist 7 ja nicht nur 4 + 3, sondern auch 8 – 1. Es existieren nämlich für die Kongruenzen – 1 nach p und + 2 nach p schon Lösungen nach Euler und Lagrange, während für die Kongruenzen 0 nach p und + 1 nach p die Fälle trivial sind. Wir nähern uns jetzt den Welträtseln. |
|
Ich habe bewusst das Beispiel – 198 gewählt, weil es die Anwendung beider Ergänzungssätze erlaubt und erkennen lässt, dass Gauß im Alter von 19 Jahren nicht bemerkt hat, dass er da gar keine Primzahlen kürzt, sondern mit logarithmischen Primzahlen hantiert. Wäre in den großen Zeiten der Kernchemie bekannt gewesen, dass es über die Primzahlen – 1 und + 2 die Möglichkeit gibt, Logarithmen zu verkleinern, wären die 4 radioaktiven Zerfallsreihen unter einem ganz anderen Blickwinkel betrachtet worden. Sie gehorchen nämlich den 4 Reihen |
|
|
Die Physik kennt 4 Kräfte im Kosmos. Die 3. und 4. Kraft ordnen wir jetzt dem 4- dimensionalen Raum zu und wenden uns zum Geheimnis der starken Kernkraft und der schwachen Wechselwirkung als einem logarithmischen Problem. Die schwache Wechselwirkung haben wir gerade beispielhaft erfasst. Für sie bleibt nur die Frage offen: Warum sind die beim Protonenzerfall ausgestoßenen Positronen und die beim Neutronenzerfall ausgestoßenen Elektronen nicht alle energetisch gleich, wie das bei den α –Teilchen der Fall ist?
Wolfgang Pauli, den sie das Gewissen der Physik nannten, war Trinitarier im Sinne von Kepler und gleichzeitig Quarternianer im Sinne von Fludd. Er hat die Einsteinsche Raum- Zeit- Verknüpfung als Nessushemd bezeichnet und war über die Vierfachheit der Basen der DNA, die er mit den 4 Quantenzahlen der Elektronen verglich schier aus dem Häuschen. Fast hätte er für die Postulierung der Antineutrinos, die 1955 nachgewiesen wurden, den zweiten Nobelpreis erhalten. Welche Masse haben die Neutrinos? Ich werde zeigen, dass sie imaginäre Ereignisse sind und damit die Masse 0 haben müssen, weil sie logarithmisch dem Exponenten 00 entsprechen. |
Kommen wir zur starken Kernkraft. Da sich Protonen unvorstellbar heftig abstoßen müssten, hat man versucht, den Neutronen die Rolle eines Klebstoffes zuzuordnen. Für das Pion als Austauschteilchen hat es gar den Nobelpreis gegeben. Ich habe nun diesem Unfug ein Ende gesetzt und die Masse, die ein Neutron besitzt einer gewissen Menge an reziprokem Raum zugeordnet. Die elektrische Ladung beträgt 0, was eigentlich die Logik verletzt, weil eine Ladung 0 ein Widerspruch in sich selbst ist. Es lag doch auf der Hand, dass die elektrische Ladung auf der Oberfläche liegt, aber nicht-euklidisch auf der Kugeloberfläche und zudem komplex.
Gauß hat von Elektromagnetismus mehr gewusst, als wir bis heute ahnen. Verlässt das Elektron mit der Ladung – 1 die Quadropol- Geometrie der 3- dimensionalen Kugel, fliegt es als punktförmiges Teilchen aus dem Kern. Es kann nicht mehr zurück, da um den Atomkern ein 4- dimensionaler Raum mit Hüllengesetzen herrscht, der die punktförmige Ladung wie eine Welle behandelt. Gleichzeitig mit der Emission des Elektrons wird der komplexe Anteil der Oberflächenladung ein imaginäres Ereignis aussenden, was keine Masse haben darf, weil elektrische Ladung etwas mit reziproker Zeit zu tun hat. |
|
|
|
+ 2 – 1 = + 1. |
Wir wollen 4 Protonen wie auf der Sonne durch Zusammenschuss in ein Heliumatom umwandeln. Das Modell zeigt in der Mitte einen konkaven Raum, der nicht-euklidisch, komplex, transzendent und fraktal ist und folgende Form besitzt. Dieses Raum-Zeit-Zahlen-Gebilde ver-wandelt sich nach der Einstein-Gleichung E = m·c² in elektromagnetische Energie, die im 4- dimensionalen Raum nur mit einer konstanten Geschwindigkeit als Kugelwelle davon eilen kann.
|
|
|
Mit den letzten Folien kann ich Ihnen zeigen, dass wir vor einem historischen Wandel stehen. Ein Mensch hat einen Blick hinter jenen Vorhang werfen dürfen, was uns bisher verwehrt war. Arnold Sommerfeld konnte nicht erklären, warum aus einer Wirkung durch Teilen mit der dimensionslosen Konstanten 4π ein Drehimpuls wird. In Wirklichkeit muss das Plancksche Wirkungsquantum mit 1/ 4πi multipliziert werden. Wir vergleichen den Nenner 4πi mit der Gleichung für das Drehen der ganzen Zahlen auf dem Primzahlkreuz und erkennen, dass der Ausdruck diesmal im Exponenten von e steht. Da wir e als die unendliche 4- dimensionale Ordnung primzahliger Anzahlen erfasst haben und die Kernladungszahlen mit der Anzahl der Elektronen auf den Hüllen identisch sind, ist bewiesen, dass die Oberflächen-ladungen von Atomkernen Logarithmen sind. Der Kern steuert die Hülle, weil Exponenten Steuerbefehle sind.
So wie sich bei der Ableitung des Zusammenhangs zwischen Energie, Masse und der Lichtgeschwindigkeitskonstanten beim Ausrechnen die Gleichung E2 = m2c4 ergibt und ein Kürzen zu E = mc2 jeden Zusammenhang zur Vierdimensionalität gedanklich verhindert, so ist auch für einen Mathematiker die Gleichung e4πi = 12 = i8 bedeutungslos. Ich möchte diese Überlegung nicht weiter ausführen. So erhalten wir durch 2- maliges Radizieren die Euler-Relation. |
| Euler hatte bekanntlich in die Exponentialreihe die Zahl i multipliziert, um dann die alternierende Reihe in einen Sinus- und Cosinus- Anteil zu überführen. Eulers Formel ist die wichtigste Gleichung der Mathematik. Ohne sie gäbe es keine Quantenmechanik. Wir haben jetzt erfasst, dass die Gleichung vor Euler existierte. Plato hatte Recht. Hinter dieser Welt steckt ein unsichtbarer, transzendenter, mathematischer Bauplan. Die Gleichung eiπ = – 1 steuert das Verhalten von Kern und Hülle, wobei die Ordnungszahlen auf der Oberfläche nur als logarithmische Ladungsdifferenzen auftreten, während die entsprechende Anzahl von Hüllenelektronen als vorhandene Anzahlen existieren. Die Euler-Relation, die seine Zeitgenossen noch für ein Kuriosum hielten und für die meine Kollegen keine Ehrfurcht empfinden, ist das Rätsel dieser Welt. |
 |
| Abbildung 83 |