Das Primzahlkreuz und die Zahl 24
|
Das Bild zeigt den jugendlichen Karl Friedrich Gauss, der 1777 geboren wurde und im Alter von 19 Jahren sein Doktorexamen ablegte.
|
|
Schon zu Beginn der Neuzeit (1600) war das Multiplizieren und Dividieren im Dezimalsystem geläufig und auch der Begriff des Logarithmus` zur Basis e=2.71 …, ohne den man keine Wurzeln ziehen kann z.B. in trigonometrischen Berechnungen (Seefahrt). Erst Leibniz bemerkte, dass mit dem Primzahlzwilling 5 und 7 ein Sechsercode beginnt, nämlich (11,13), (17,19). Wenn einmal in einem Fach wie Mathematik etwas Grundlegendes übersehen worden ist, kann es nachträglich nicht mehr entdeckt werden, weil es ja nicht gesucht wird. Auch der Finder würde es gar nicht erfassen. Leibniz bemerkte eben nicht, dass die einzige gerade Primzahl 2 und die einzige ungerade Primzahl 3, die nicht zum Sechsertakt gehören, dazu zwingen, sie als Anfangszahlen der geraden Zweierzahlen 2, 4, 8, 10, 14, 16, … und der Dreierzahlen 3, 6, 9, 12, 15, 18, … aufzufassen. Folglich müssen die 2 und die 3 als Anfangsglieder eigener Zahlenreihen prim sein. Ungeklärt bleibt nur noch die Ziffer 1, deren Wurzel –1 beträgt. Da im Zeitalter des Barocks auch für Leibniz die Zahl –1 verboten war, weil etwas weniger als Null die damalige Logik verbot, stieß er nicht zu dem Gedanken vor, dass die Zahl –1 und ihre Spiegelzahl +1 die Anfangsglieder des unendlichen Sechsercodes sind.
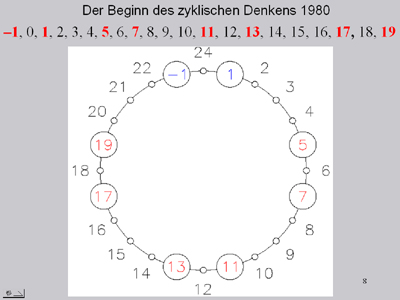
Plichta, der als erster diese vier fortlaufenden Zwillinge zyklisierte, bemerkte, dass der geschlossene Kreis nach der 19 noch bis zur Zahl 24 fortgeführt werden muss. Auf dem ersten Kreis liegen also an der Stelle –1 auch die 23 und an der Stelle 24 ebenfalls die Ziffer 0. Oberhalb der 1 wird mit den 25 Ziffern 24 – 48 die Zahl 25 liegen, das Quadrat der vorrausgegangenen 5. Darüber liegt die Zahl 49, die auch eine Quadratzahl ist, nämlich 72. Später folgen auf dem Strahl oberhalb der 1 sämtliche weiteren Quadratzahlen 112, 132, 172, 192, 232, 252 … . Die letzte Ziffer kann man auch als 54 schreiben und daraus schließen, dass auf dem 1er-Strahl sämtliche geradzahlige Exponenten der Basiszahlen liegen, die den Sechsertakt der Primzahlen steuern.
 Das Foto zeigt Carl Friedrich Gauß 1803 im Alter von 26 Jahren. Er begann sein Mathematik-studium im Alter von 17 Jahren und promovierte mit 19. Gleichzeitig hatte er zu diesem Zeitpunkt sein großes Vorbild Leonhard Euler mit dem genialsten Werk der Mathematikgeschichte weit überholt (Disquisitiones Arithmeticae - Beiträge zur Zahlentheorie). Gauß war ein großer Schweiger, weil er seinen mathematischen Kollegen bis zur Verachtung überlegen war. Er war der erste, der es wagte die Zahl minus 1 und ihre Wurzel i als real existierend zu bezeichnen. Er hatte schon mit 15 Jahren erfasst, dass die ganze Mathematik nur auf den Primzahlen aufbaut, und dass die 1 aus zwei Zahlen besteht (er meinte +/– 1). Er erfasste als erster, dass es drei Geometrien gibt: die rechtwinklig-euklidische, die konvexe und die konkave.) Über gekrümmte (Welt-)Räume hätte er nur gelacht. Ob er erfasst hatte, dass die Natur zyklisch primzahlig angelegt ist, kann nur vermutet werden, da der Begriff der Atomschalen noch völlig unbekannt war.
Das Foto zeigt Carl Friedrich Gauß 1803 im Alter von 26 Jahren. Er begann sein Mathematik-studium im Alter von 17 Jahren und promovierte mit 19. Gleichzeitig hatte er zu diesem Zeitpunkt sein großes Vorbild Leonhard Euler mit dem genialsten Werk der Mathematikgeschichte weit überholt (Disquisitiones Arithmeticae - Beiträge zur Zahlentheorie). Gauß war ein großer Schweiger, weil er seinen mathematischen Kollegen bis zur Verachtung überlegen war. Er war der erste, der es wagte die Zahl minus 1 und ihre Wurzel i als real existierend zu bezeichnen. Er hatte schon mit 15 Jahren erfasst, dass die ganze Mathematik nur auf den Primzahlen aufbaut, und dass die 1 aus zwei Zahlen besteht (er meinte +/– 1). Er erfasste als erster, dass es drei Geometrien gibt: die rechtwinklig-euklidische, die konvexe und die konkave.) Über gekrümmte (Welt-)Räume hätte er nur gelacht. Ob er erfasst hatte, dass die Natur zyklisch primzahlig angelegt ist, kann nur vermutet werden, da der Begriff der Atomschalen noch völlig unbekannt war.
Warum spielt nun die Zahl 24 = 4! = 1 • 2 • 3 • 4 für die zyklische Verteilung der Primzahlen die entscheidende Rolle oder umgekehrt, warum kann man zum Zyklisieren nicht einfach eine andere Zahl nehmen, z.B. 36? Der Beweis ist einfach. 52 = 25 minus 1 ist 24. Für 72 = 49 gilt 49 minus 1 ist 48, also 2 • 24. Für das Quadrat der 11 gilt 121 minus 1 ist 120, also 5 • 24 und für 132 gleich 169 gilt, dass 168 sieben mal 24 ist usw. Die geheimnisvollen Primzahlen, über die man glaubt alles zu wissen außer der ungelösten Riemanschen Vermutung, sind in Wirklichkeit nie in ihrer richtigen Bedeutung erkannt worden. Durch den oben genannten, linearen Sechsertakt entsteht in der Quadratur eine sich erweiternde, schalenförmige Zahlenebene, die die Quadrate des linearen Sechsertaktes alle auf dem selben Strahl oberhalb der 1 beinhalten.
Welche Zahlen liegen noch auf dem Einserstrahl? Nun alle Produkte von zwei Zahlen, die sich auf einem Strahl der insgesamt acht Strahlen befinden. Beispiel: 7 • 103 = 721. Die 103 ist gleich 96 plus 7. Da 96 ein Vielfaches von 24 ist, müssen die beiden übrig gebliebenen Zahlen 7 und 7 den Grund dafür liefern, dass sich 721 auf dem Strahl über der 1 befindet. Man kann nun 721 in 720 + 1 zerlegen und erhält 6! +1. (6! muss sich oberhalb der 24 = 4! finden.) 6! + 1 lässt sich schreiben als
also als Beispiel für den Satz von Wilson. Dies ist der einzige Satz, der nur für Primzahlen gilt. Euler hat ihn als erster bewiesen und niemand weiß, warum es diesen Satz gibt. Plichta hat es sich zur Aufgabe gemacht, die wichtigsten mathematischen Sätze, die alle bewiesen sind, darauf hin zu untersuchen, warum es sie gibt. Nach Abschluss seiner Arbeiten steht fest, warum die Primzahlen von der Form 6n ± 1 nach dem natürlichen Logarithmus zur Basis e abnehmen (Gauß, Hadamard u.a.) und warum π etwas mit einer Produktformel zu tun hat, die nur Primzahlen enthält, und die sich nach Herausnahme der Faktoren 2 und 3 in eine Produktformel verwandeln lässt, die auf dem Vielfachen von 24 basiert und den Wert π2 / 32 besitzt. (Eulersche Zeta-Funktion)
Fazit: Während die wirklich großen Mathematiker Newton, Leibniz, Euler und Gauß den Zahlen noch irgendwie göttliche Attribute zuordneten, gelten sie heute als rein menschliche Erfindungen. Da sie sich aber nur in einem Stellenwertsystem sinnvoll anwenden lassen, wird das Dezimalsystem dem Zufall zugeordnet, der etwas mit der Anzahl unserer Finger zu tun hat. Indem Plichta den Schalenraum des vierdimensionalen Primzahlkreuzes als dezimal angelegt erfasste, legte er sich mit Berufsmathematikern an, denen Zahlen an sich vollkommen gleichgültig sind und denen jeder Zusammenhang zwischen Zahlen und Geometrie auf der einen Seite und ihr Bezug zu den Naturwissenschaften Chemie, Physik, Kernchemie und Biologie unbegreiflich ist, einfach weil sie von diesen Fächern schlichtweg keine Ahnung haben. In einigen Jahren wird man über unser Zeitalter und seine Auswüchse wie Urknall, Superstrings, Quarks und Zufall den Kopf schütteln, sowie das heute über christliche Dogmen oder die Alchemie Gang und Gäbe ist. Wir haben eben nie etwas aus der Geschichte gelernt: Da wo der Zweifel stirbt, stirbt die Wissenschaft.

